Nested squares

I saw this animation on Twitter, and thought it would be a good candidate to implement in Processing. This version uses transformations like scale() and rotate() to create iterative changes throughout the pattern.

While easy to implement, because the canvas is being transformed, it also has some drawbacks:

Although all that’s being drawn is simple squares, I don’t think I could easily draw these squares with the plotter.
Heavy use of transformations (perhaps without fully understanding pushMatrix() and popMatrix() interferes with other elements, particularly the GUI elements from the ControlP5 library.
The code is complicated by compensation factors that need to be added to counteract some aspects of the transformations.

Sketch: `nested_squares_3b/nested_squares_3b.pde`

Here’s an animated version:

In code, one nest looks like this. First draw one square:

pushMatrix(); // store setup of first square      
// draw first unaltered square
lineThickness = initialLineThickness;
translate(xStart, yStart);
strokeWeight(lineThickness);
fill(255);
stroke(0);
rect(0, 0, squareWidth, squareHeight);

Then iterate through the remaining squares in the nest, rotating each one a little bit each time:

for (int i = 0; i < numberOfNestings -1; i++) { // 1st square is already drawn
  strokeWeight(lineThickness);
  rotate(radians(rotateAngle));
  scale(scaleFactor);
  fill(color(constrain((255-(i*5)), 0, 255)));
  rect(0, 0, squareWidth, squareHeight);
  
  // after drawing, scale all the affected factors to compensate for the transformations
  nextSqareIndentation = nextSqareIndentation / scaleFactor;
  lineThickness = lineThickness / scaleFactor;
}   

Then reset for the next square:

popMatrix(); // reset for a new nest
rotateAngle = -1 * rotateAngle; // flip the rotation. 

There are a few tricky bits. The amount of rotation (rotateAngle) to apply is derived from the distance along the square edge you decide to start the next square (nextSqareIndentation). The rotation amount then determines how much to scale the next square so that it fits precisely inside the previous one.

float nextSqareIndentation = (squareWidth/(numberOfNestings)) * 0.2; // get crazy effects by increasing this massively...
float rotateAngle = degrees(atan(nextSqareIndentation/(squareWidth - nextSqareIndentation)));
float newWidth = sqrt(sq(nextSqareIndentation) + sq(squareWidth - nextSqareIndentation));
float scaleFactor = newWidth / squareWidth;

Here’s how I did the maths – after much head scratching…

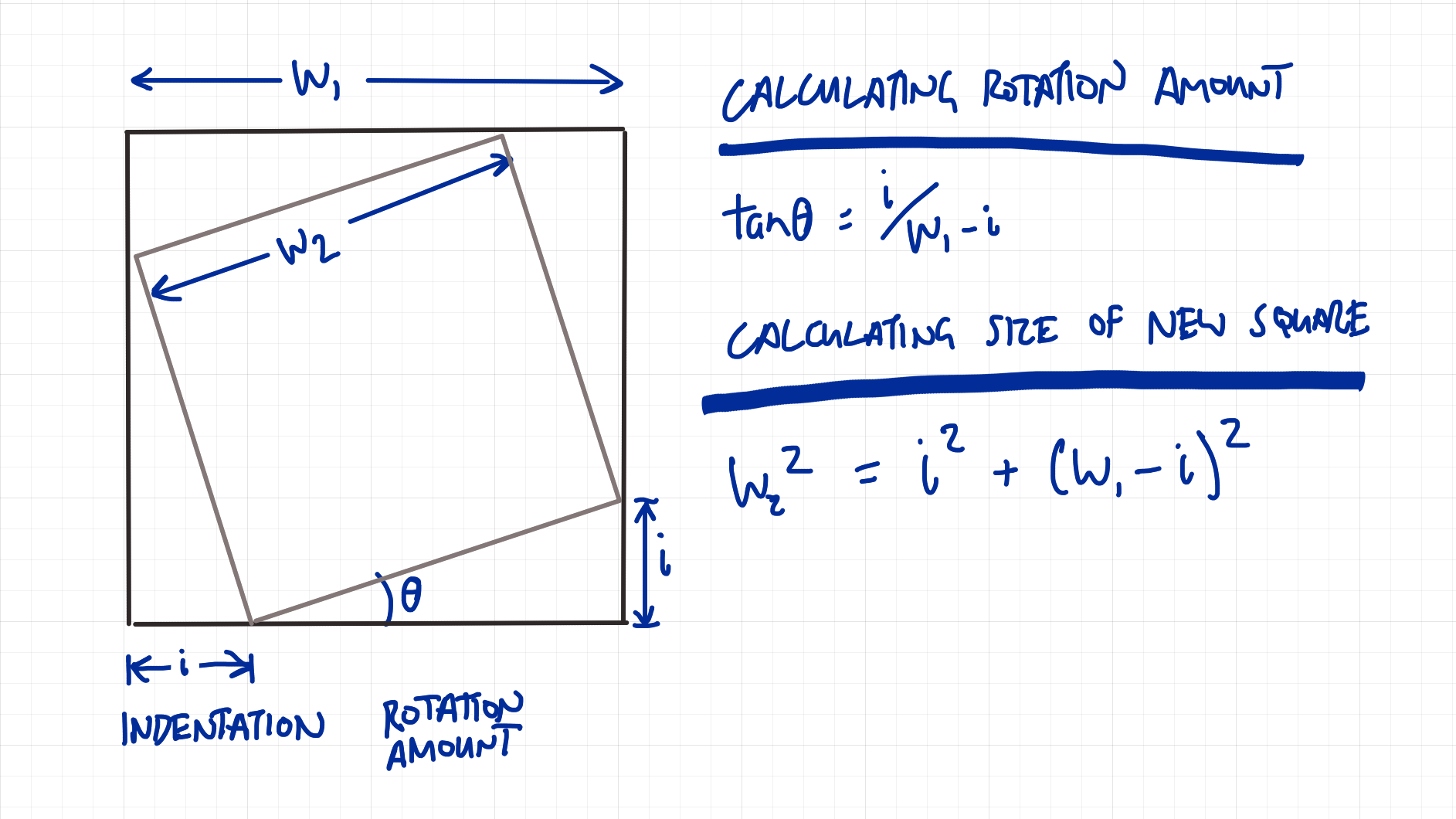
You can see from the first line that I’m trying to calculate the amount of indentation by dividing the square width by the number of squares in the nest. This doesn’t quite work as expected. Because the squares rotate, their edges form spirals, which are much longer than the largest square width. And this disparity increases the greater the nesting.

I’m applying a constant multiplier to try to get the squares to fill up all the available space. I think because of the ever decreasing scale, this may never happen.

Also, if you make the multiplier too high, it can calculate (for small nestings) an indentation amount which is longer than the entire width of the square, which causes the squares to grow instead of shrink.

Finally, I realised for version 3c that I need to move these calculations into the draw() loop, as I’m altering the numberOfNestings parameter live, using the GUI controls.

Sketch: nested_squares_3b/nested_squares_3b.pde

Sketch: `nested_squares_3b/nested_squares_3b.pde`